The 3D Etch A Sketch (with the Fourier Transform and Epicycles)
Zoom in and out using mouse scroll | Move by clicking & dragging or WASD | Press R to restart drawing
Explanation
"There is order in chaos"
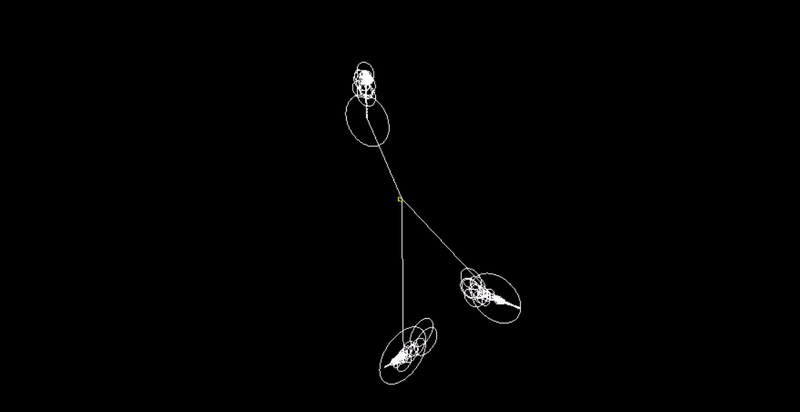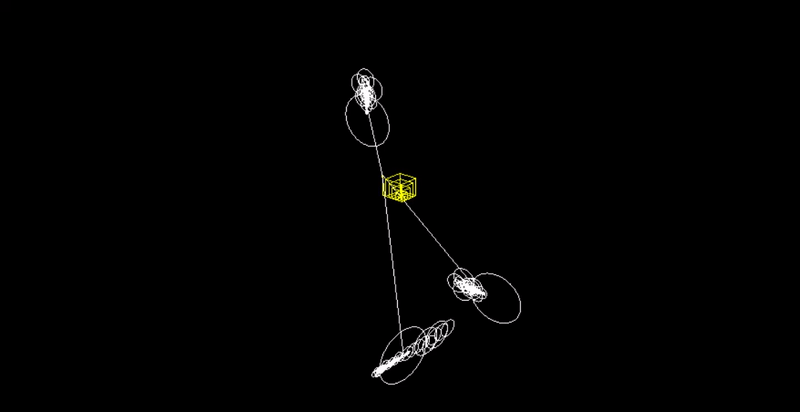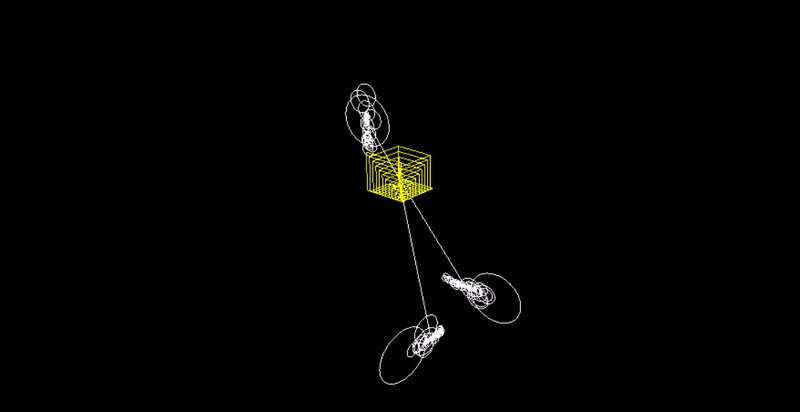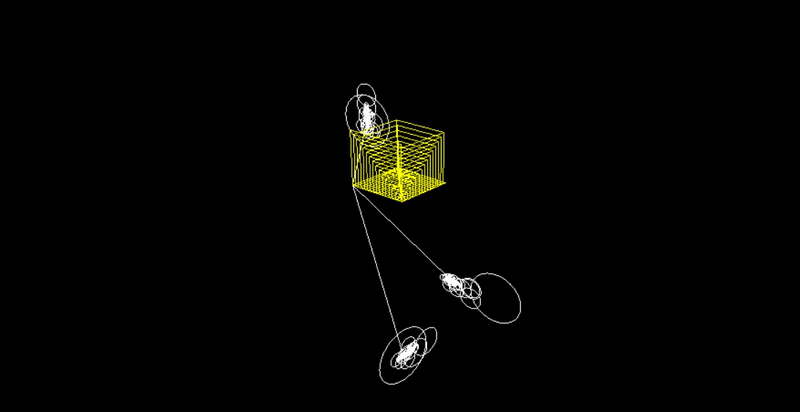
Can we create a drawing machine that takes in any ordered set of $3D$ points and draws it using epicycles (a sequence of chaotic, rotating circles)?
To solve this, we must do the following:
Step 1. Take our $3D$ points and create $3$ functions from its $x$, $y$, and $z$ components.
drawing $= {(0, 0, 1), (0, 1, 2), (1, 1, 2), (1, 0, 1), ...}$
$x = {0, 0, 1, 1...}$
$y = {0, 1, 1, 0...}$
$z = {1, 2, 2, 1...}$
Step 2. Apply the Fourier Transform to each function. This will allow us to represent each function as a sum of revolving circles and vectors. We will use the discrete version of the transform because computers cannot sum up an infinite number of values.
Step 3. Save the output of the Fourier Transform, which is a set of frequencies, amplitudes, and phase shifts. Visually, this is just a circle.
Step 4. Create $3$ epicycle systems from the output above. Each system controls the $x$, $y$, or $z$ coordinate of the points being redrawn.
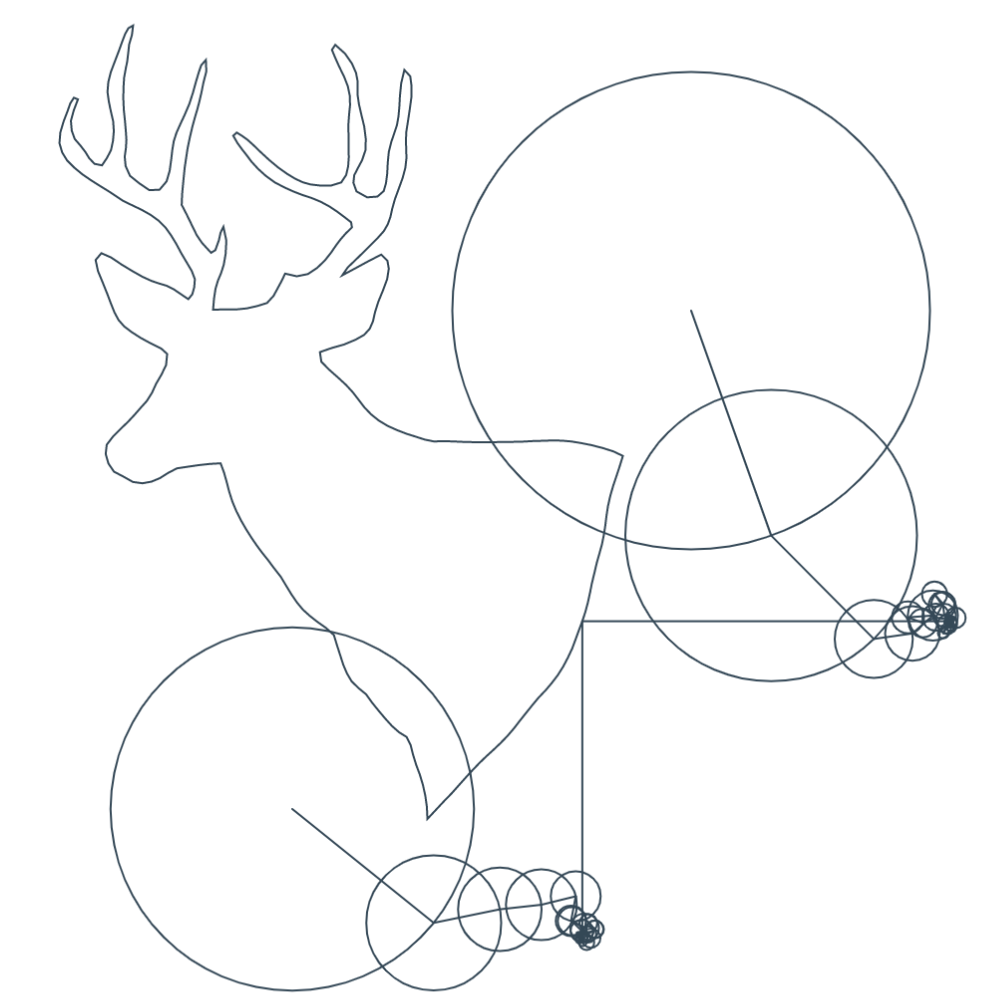
Step 5. Start an animation that goes from $t = 0$ to $t = 2*pi$. For the $3$ epicycle systems, we sum up $A * cis(f * t + phi)$, where $A$ = amplitude, $f$ = frequency, $t$ = time, $phi$ = phase shift, and $cis(theta) = cos (theta) + i sin(theta)$. We then use the real or imaginary component of the $3$ sums to create a $3D$ point, which is plotted.